2020.12.4

第10回の試験問題について、ご質問をお寄せいただき有難うございました。

以下に、お寄せいただいたご質問・ご意見について回答申し上げます。

 

●３級・問１４について

【問題文】 肉眼（にくがん）で見える星は、銀河系（ぎんがけい）（天の川銀河）のほんの一部でしかない。肉眼で明るく見える星のある範囲（はんい）の半径は、 銀河系全体の半径と比較（ひかく）するとどれくらいか。

①10000分の1

②1000分の1

③100分の1

④10分の1

 

【正解】
③100分の1

 

【解説】
肉眼（にくがん）で明るく見える星は、ほとんどが地球から1000光年くらいの範囲（はんい）にある。銀河系（ぎんがけい）全体の大きさは、まだ議論（ぎろん）が続いているものの、大ざっぱに10万光年と考えられている。よって都会でも見えるような明るい星のある範囲は、銀河系全体の50分の1より小さい＝ざっと100分の1程度である。ちなみに1万光年以上離（はな）れていても、肉眼で見える星は存在（そんざい）する。

 

【質問】
「銀河系全体の半径」とあるのは「直径」の間違いではないでしょうか。解答にも「銀河系全体の大きさは、まだ議論が続いているものの、大ざっぱに10万光年と考えられている。」とあり、テキストでも直径10万光年とされています。また、ハローの広がりは15万光年とされており、どの数字を使うかで考え方が違ってきます。全員正解とすべきではないでしょうか。

 

【回答】
この問題は、おおざっぱな値（あたい）（天文学ではオーダーとよびます）を把握（はあく）して、どちらの桁（けた）に近いかを判断（はんだん）してもらう問題です。星のある半径を1000光年として、銀河系（ぎんがけい）の直径と比較（ひかく）すれば、確かに100分の1と、すっきりした数値になりますが、あえてイメージがわきやすいように、どちらも半径で比較し、どちらがより近いかを判断していただく問題になっています。星のある範囲（はんい）を1000光年とすると、銀河系の半径と比較した場合、50分の1になります（ハローの15万光年を採用（さいよう）するなら75分の1）。これが100分の1に近いのか、10分の1に近いのかを判断します。100分の1と比較すると2倍のずれ、10分の1と比較すると5倍のずれになります。したがって、オーダーで考えると、10分の1ではなく100分の1となります。このような趣旨（しゅし）の問題であり、問題がまちがっているわけではありません。

 

●２級・問１と問題訂正について

【ご意見】
〇今回は問題訂正が4問あり、突合せに時間がかかりました。このような時は時間を5分延長するといったような対応も必要かと思いました（ご質問文より一部抜粋）。
〇公式テキストには記載があったようですが、テキストを使って勉強していない者にとっては混乱する問題でした。また、訂正があったためパニックになったという声も受験後聞いたので、全員正解などの対応をして欲しい（ご質問文より一部抜粋）。

【回答】
ご意見ありがとうございます。２級問題に複数の訂正があり、受験者のみなさまに混乱を招いたことを深くお詫びします。また、2～4級の出題は公式テキストの内容から出題すると事前に告知しておりますが、今後は告知の徹底をさらに図る所存です。いただいたご意見は次回の参考にさせていただきます。

 

●２級・問１０について

【問題文】 アニメ『機動戦士ガンダム』シリーズでよく登場するスペースコロニーでは、どのようにして重力と同じ働きをする力を得ようとしているか。

①マイクロブラックホールを搭載している

②超高速で回転するジャイロを搭載している

③スペースコロニー自体が並進加速度運動をしている

④スペースコロニー自体が回転している

 

【正解】
④スペースコロニー自体が回転している

 

【解説】
スペースコロニーは1969年にジェラルド・オニールが提唱した宇宙空間の人工居住地で、スペースコロニー自体を回転させることで遠心力による擬似重力を得ることが考えられている。例えば直径6.4kmのスペースコロニーが、110秒で１回転すれば地球と同程度の疑似重力が得られるが、回転と同じ方向に移動すれば疑似重力は大きくなり、横方向であればコリオリの力を受ける。例えばコロニー内で野球をすると、野球場の向きによって打球の行方が大きく変わるとの試算もある。

 

【質問１】
ガンダムというアニメ内のァンタジーの世界の中のスペースコロニーを問う問題と読み取れる文章でした。一般的なスペースコロニーの設問だとしても設問として生かすにはおかしい文章でした（ご質問文より一部抜粋）。

【質問２】
なぜ高速回転させてはいけないのでしょうか？ガンダムを知らない私にとっては解きにくい問題でした…（ご質問文より一部抜粋）

 

【回答１】
問題文として分かりづらい表現であったこと、また問題と共にコロニーの図を掲載するなど配慮がたらなかったことをお詫びします。『機動戦士ガンダム』に登場するスペースコロニーは、アニメの創作ではなく、そもそもオニールのスペースコロニーを参考にしています。

【回答２】
テキストP.138に、「『機動戦士ガンダム』などアニメにも取り上げれられている。」と記述があるように、そこに登場するスペースコロニーは、アニメの創作ではなく、そもそもオニールが提唱したスペースコロニーを参考にしています。②は、ジャイロが高速回転するだけで、スペースコロニー自体が回転するとは限りません。スペースコロニー自体が回転しないと、疑似重力はつくれないので、②は誤りです。

 

●２級・問４０について

【問題文】
1光年は1天文単位の約何倍になるか。

①1000倍

②10万倍

③100万倍

④1億倍

 

【正解】
②10万倍

 

【解説】
1天文単位は1.5×1011mで、1光年は9.5×1015mなので約10万倍違う。さらに、1光年の10万倍が銀河系のサイズ（約10万光年）になる。

 

【質問】
問40は選択肢が雑すぎるのではないでしょうか。3級テキスト6章のコラムに載っていますが、「1天文単位は1.5億km、1光年は10兆km」で、これを覚えて計算してきました。割り算をすると66666倍で、約7万倍ということになります。それを約10万倍と答えさせるのは、ほかの厳密な計算問題と比べても整合性が取れません。そもそもこれは2級レベルではなく、3級レベルでは？もやもやとしています（ご質問文より一部抜粋改変）。
【回答】
この問題は、おおざっぱな値（天文学ではオーダーと呼びます）を把握してもらうもので、天文学的な捉え方、概算という概念を理解していただく意図で出題いたしました。ご意見ありがとうございます。今後の参考にさせていただきます。

 

●１級・問１４について

【問題文】

低質量の主系列星の光度は、質量のおよそ3乗に比例する。この場合、太陽の質量の0.5倍の主系列星の寿命はどれくらいか。なお、太陽の寿命を100億年とする。

①200億年

②400億年

③600億年

④800億年

 

【正解】
②400億年

 

【解説】
質量をM、光度をLとすると、質量光度関係はL＝M3と表される。主系列星の寿命τは質量を光度で割った値に比例するので、τ∝M /L ∝M /M3＝M－2となり、寿命は質量の2乗に反比例する。したがって、太陽の質量の0.5倍の主系列星の寿命は、

τ＝100億年×（0.5）－2＝100億年×22＝400億年となり、②が正答となる。

 

【質問１】
公式問題集によると星の明るさはコードLは3乗から4乗に比例すると書いてあります。星の寿命のτはL分のMに比例するから星の質量Mをコードで割ったものになり、質量の3乗から4乗分のMの3乗から4乗分のMだからMの2乗から3乗分の1になります。太陽の質量の2分の1の寿命はどれかっていうと4分の1から8分の1になります。答えは400億年から800億年の範囲になるから解答は③600億年を選びましたが解答は②400億年ということになるとのことですが、一度お調べいただけないでしょうか。

 

【回答１】
多くのテキストなどには、「主系列星の光度は質量の3～4乗に比例している」と書かれていますが、これは、横軸に質量の常用対数値を、縦軸に光度の常用対数値をとってプロットすると、全体的にほぼ直線状に分布し、その傾きが3～4の間にあることを意味しています。しかし、その分布を詳しくみると、低質量側で傾きが小さく3に近くなり、質量が大きいと傾きが4に近くなります。
この問題では、「低質量の主系列星の光度は質量のおよそ3乗に比例する」と規定しており、「質量が太陽の0.5倍」と、主系列星も低質量側にありますので、3乗で計算した結果を正答としています。1級公式参考書『極・宇宙を解く』の「第３章 恒星の世界　27．主系列星の質量光度関係」の項に詳述してありますので、ご参照ください。

 

【質問２】
上記回答で、「しかし、その分布を詳しくみると、低質量側で傾きが小さく3に近くなり、質量が大きいと傾きが4に近くなります。(中略)1級公式参考書『極・宇宙を解く』の「第３章恒星の世界　27．主系列星の質量高度関係」の項に詳述してありますので、ご参照ください。」とありますが、公式参考書P.114の(27.6)式によると、質量が小さく低温の恒星では、光度は質量の5乗に比例する旨が書かれており、逆に質量の大きな恒星は質量の3乗に比例することが書かれています。回答の内容は、テキストの内容と矛盾していませんか。問題文には確かに「低質量の主系列星の光度は、質量のおよそ3乗に比例する。」ことが前提とされており、それを前提にすれば答えは導かれますが、そもそもの前提がテキストの内容と違うことにかなり違和感を覚えました。

 

【回答２】
ご指摘の通り、確かにテキスト（極・宇宙を解く）には、「低質量側で光度の5乗に比例する」と書いてあります。この部分は、理論的な導出が述べられていますが、理論的な考え方をおおざっぱな見積もりで示したものです（例えば、中心温度は一定とするなど）。
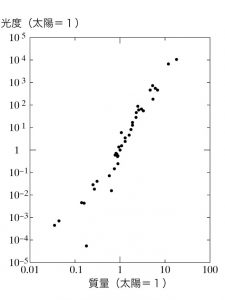
他方、観測的に見ますと、参考図1に示すように、低質量星側では傾きは少し小さめになります。この図は、テキストの演習のデータを使って作成したものです。

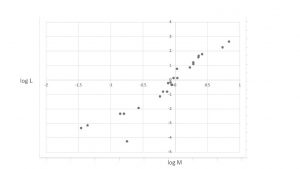
また、大質量星のデータは少ないですが、別の資料から作成したものも示します（参考図2）。観測的には、低質量星側と大質量星側で少し傾きが変化することがわかると思います。

問14は、このような観測事実をもとにして作成しましたが、テキストの記述と矛盾がありました。
テキストの理論的見積もりは、簡単な見積もりで質量光度関係がだいたい導けること、低質量星側と大質量星側で異なることを示したものです。観測的には、上述の回答どおりです。観測的な事実と、テキストの理論的導出の結果が矛盾してしまったのは、テキストの理論的な導出が粗いためだと考えてください。
頂いたご意見はテキスト改訂時に、参考にさせていただきます。

 

●１級・問４０について

【問題文】
南天の星座に「ぼうえんきょう座」がある。これは、南天の観測を終えたニコラ＝ルイ・ド・ラカイユが作成した14の星座の1つで、1756年に彼の星図で表記された。この「ぼうえんきょう座」の望遠鏡は何がモデルになっているとされているか。

①ガリレオ・ガリレイの作った望遠鏡

②アイザック・ニュートンの作った反射望遠鏡

③ウィリアム・ハーシェルの巨大反射望遠鏡

④ジャン＝ドミニク・カッシーニが使った空気望遠鏡

 

【正解】
④ジャン＝ドミニク・カッシーニが使った空気望遠鏡

 

【解説】
ぼうえんきょう座は、いて座やみなみのかんむり座の南にある星座で、暗い星ばかりでできている目立たない星座である。ラカイユは当時、土星のカッシーニの隙間など様々な発見をしていたパリ天文台のジャン＝ドミニク・カッシーニ（1625–1712）の望遠鏡をモデルにしたとされている。実際ヨハン・ボーデの星図などには、長い望遠鏡が描かれており、ニュートンの反射望遠鏡やガリレオの望遠鏡とはあきらかに違う。なお、ハーシェルが活躍したのは1773年以降で、有名になったのは1781年の天王星発見。巨大望遠鏡の建設はさらに後の1785年以降に作られている。

 

【質問】
設問40の正答が選択肢④カッシーニの空気望遠鏡であること自体に疑義はありません。キーワード｢ぼうえんきょう座｣だけで検索してもその旨の記述が複数見つかること、ラカイユとカッシーニの関係、ぼうえんきょう座が作られた当初は現在より遥かに長い領域だったこと、競うように｢ハーシェルのぼうえんきょう座｣が作られたことなどから、納得できます。しかし、ぼうえんきょう座が作られた当時の古星図はともかく、現在書店や図書館にある書籍の多くに採用されているぼうえんきょう座の星座絵は、ほぼ全部が空気望遠鏡ではなく鏡筒がある屈折望遠鏡に見える形状に描かれており、選択肢①ガリレイの望遠鏡を参考にしたと思われるものも複数見受けられます。神話が無いため、由来に言及していない本も少なくありません。ということで、①ガリレイの望遠鏡が選択肢にあるのは｢引っ掛け問題｣の範疇を超える紛らわしさに思え、｢メシエの望遠鏡(監視者メシエ座が作られたことがある)｣にでもしていただいた方が疑義の余地を無くせたかと思われるのですが、いかがでしょうか。

 

【回答】
「ラカイユが作成した星座は1756年に彼の星図に表記された」と問題中にヒントがあります。彼は同時代・少し前の機器を星座としてとりあげています。時代的に、ガリレイ、ニュートン、ハーシェルは排除するためのヒントになるので誤答として設定しています。有名な天文学者とその時代、星座の成立などから、仮に知らなくても、類推できる問題と考えています。